- Innovaciones
- Artículos sobre la aplicación de PCI
- Trading de Portfolios
El Método de Cotización del Portafolio para el Análisis de Portafolios "buenos" y "malos"
La crisis financiera mundial de 2008 afectó a todos los sectores de actividad económica, sin excepción. Afectó a las empresas como así a sus resultados empresariales, tanto directa como indirectamente, pero el nivel de impacto fue diferente. Este hecho ofrece grandes oportunidades para encontrar estrategias de inversión basadas en las diferencias en la reacción de los precios de las acciones a largo plazo; por ejemplo, el stock sobre el factor sistemático.
En este artículo vamos a tratar de encontrar un ejemplo de una cartera que estadística y gráficamente refleje la posibilidad de construir una estrategia de éxito en las inversión sobre la base de las diferentes comportamientos de la población a largo plazo. Para ello, se seleccionaron 22 poblaciones de los Estados Unidos, Empresas grandes y con liquidez, pertenecientes a los distintos sectores de la economía Norteamericana. Utilizando los métodos de la teoría moderna, los principios de diversificación de riesgos , así como el método de cotización del portafolio (PQM), vamos a tratar de dividir los activos seleccionados en 2 grupos: las carteras “buenas” y “malas”, como también, el método de análisis de la cartera GeWorko, donde trataremos de dividir los activos seleccionados en 2 grupos de similar denominación: las carteras “buenas” y “malas”.
La "buena" cartera se compondrá de activos con pesos positivos, es decir, los que son candidatos para la compra. La cartera “mala” incluirá acciones de posiciones cortas, las que deben tomarse de acuerdo a nuestro análisis. Todo el análisis se basa en los precios de los cierres mensuales, y sus variaciones en los últimos 4 años (50 meses). La composición de los activos (22 acciones), es seleccionada para construir una cartera, con sus boletines correspondientes, nombres de empresas y sectores económicos que se dan a continuación:
Tabla 1: Nombres de empresas y sectores económicos de las acciones seleccionadas
| # | Ticker | Company | Sector |
| 1 | AA | AlcoaInc | BasicMaterials |
| 2 | AXP | AmericanExpressCompany | Financials |
| 3 | BA | BoeingCompany | Industrials |
| 4 | DD | DupontCompany | BasicMaterials |
| 5 | DIS | WaltDisneyCompany | CyclicalConsumerGoods&Services |
| 6 | GE | GeneralElectricCorporation | Industrials |
| 7 | HD | HomeDepotInc | CyclicalConsumerGoods&Services |
| 8 | HON | HoneywellInternationalInc | Industrials |
| 9 | HPQ | Hewlett-PackardCompany | Technology |
| 10 | IBM | InternationalBusinessMachineCorp | Technology |
| 11 | INTC | IntelCorporation | Technology |
| 12 | JNJ | Johnson&Johnson | Healthcare |
| 13 | JPM | JP MorganChase&Company | Financials |
| 14 | KO | Coca-ColaCompany | ConsumerNon-Cyclicals |
| 15 | MCD | McDonaldsCorporation | CyclicalConsumerGoods&Services |
| 16 | MRK | MerckCoInc | Healthcare |
| 17 | MSFT | MicrosoftCorporation | Technology |
| 18 | PFE | PfizerInc | Healthcare |
| 19 | T | AT&T | Telecommunication |
| 20 | VZ | VerizonCommunicationsInc | Telecommunication |
| 21 | WMT | Wal-MartStoresInc | CyclicalConsumerGoods&Services |
| 22 | XOM | ExxonMobilCorporation | Energy |
Sobre la base de los datos mensuales, vamos a calcular valores realizados de la rentabilidad media, la desviación estándar de la rentabilidad, y una versión simplificada de la ratio de Sharpe para cada serie de datos.
Los resultados de los cálculos de las rentabilidades mensuales medias y las desviaciones estándar se muestran en la siguiente tabla:
| Asset | MeanReturn | StandardDeviation | Asset | MeanReturn | StandardDeviation |
| AA | 0.31% | 10.60% | JNJ | 1.01% | 3.76% |
| AXP | 3.32% | 10.96% | JPM | 1.27% | 9.05% |
| BA | 1.99% | 6.96% | KO | 1.31% | 4.16% |
| DD | 1.81% | 7.90% | MCD | 1.22% | 3.68% |
| DIS | 2.58% | 6.54% | MRK | 1.11% | 5.28% |
| GE | 1.64% | 8.48% | MSFT | 1.20% | 6.67% |
| HD | 2.33% | 6.41% | PFE | 1.54% | 4.85% |
| HON | 2.05% | 6.40% | T | 0.78% | 4.16% |
| HPQ | -0.80% | 10.36% | VZ | 1.27% | 4.83% |
| IBM | 1.49% | 4.27% | WMT | 0.83% | 4.17% |
| INTC | 0.92% | 6.59% | XOM | 0.58% | 4.65% |
Además, se puede calcular una versión simplificada de la ratio de Sharpe para cada activo. La relación resulta de dividir el retorno por la desviación estándar mostrando el rendimiento por unidad de riesgo. Estos coeficientes serán una buena guía para nuestro análisis con el fin de determinar la eficacia de la estrategia de inversión. Los coeficientes resultantes se muestran en el diagrama:
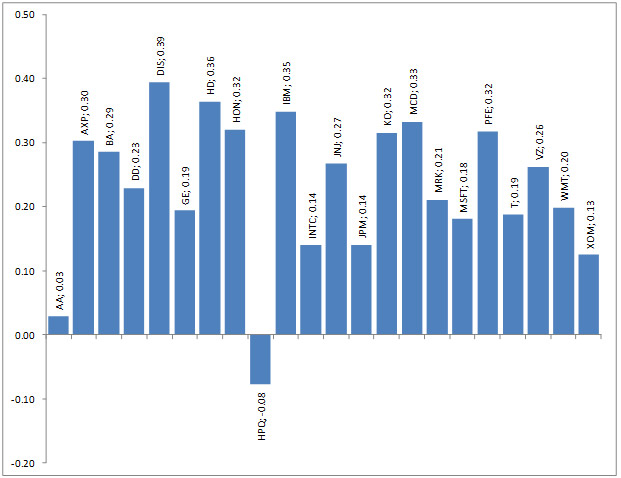
La siguiente etapa del análisis es encontrar los coeficientes de peso óptimos para cada activo y de construir una cartera de valores. El criterio de optimización de la cartera puede ser el ratio de Sharpe, el parámetro de retorno, o su desviación estándar. En nuestro caso, el criterio de optimalidad será la cartera del posible máximo retorno esperado, realizables en todos los niveles de la desviación típica no mayor que el promedio de desviación estándar para la muestra de 22 acciones. La desviación estándar media de las 22 acciones es 6,40% y queremos que nuestra cartera no sea más riesgosa que sus activos constituyentes en promedio. Para el cálculo de los coeficientes de peso, también necesitaremos la covarianza de los activos, que indican el nivel de interrelación entre cada par de activos.
El procedimiento de optimización de peso (que tiene dos limitaciones: la máxima desviación estándar de la cartera (6,40%) y la suma final de los pesos, que debe ser 100%) nos lleva a la siguiente solución, lo que maximiza el rendimiento de la cartera:
| Asset | Weight | Asset | Weight |
| AA | -70.27% | JNJ | 21.59% |
| AXP | 8.97% | JPM | -31.82% |
| BA | -4.39% | KO | 29.55% |
| DD | -22.00% | MCD | -15.80% |
| DIS | 88.08% | MRK | -5.98% |
| GE | -41.55% | MSFT | 51.73% |
| HD | 37.01% | PFE | 39.28% |
| HON | 145.66% | T | -96.14% |
| HPQ | -43.92% | VZ | 81.77% |
| IBM | 152.36% | WMT | -56.03% |
| INTC | -39.34% | XOM | -128.76% |
Dado que no hemos puesto restricciones a la posibilidad de ventas cortas de activos, la solución ofrece dos pesos positivos y negativos. Los activos con pesos positivos, condicionalmente llamada "buena" y los que tienen carteras de peso "malo" o negativos. Vamos a agrupar a los activos de acuerdo a su nueva clasificación:
| GoodPortfolio | BadPortfolio |
| Asset | Weight | Asset | Weight |
| AXP | 8.97% | AA | -70.27% |
| DIS | 88.08% | BA | -4.39% |
| HD | 37.01% | DD | -22.00% |
| HON | 145.66% | GE | -41.55% |
| IBM | 152.36% | HPQ | -43.92% |
| JNJ | 21.59% | INTC | -39.34% |
| KO | 29.55% | JPM | -31.82% |
| MSFT | 51.73% | MCD | -15.80% |
| PFE | 39.28% | MRK | -5.98% |
| VZ | 81.77% | T | -96.14% |
| WMT | -56.03% | ||
| XOM | -128.76% |
Hay un poco más de activos "malos" que de "buenos", sin embargo, como un epíteto, no disminuye su importancia. Como veremos más adelante, estos dos grupos de activos son capaces de mostrar los resultados más eficaces sólo cuando están juntos. En cuanto a las empresas 'que pertenece a un sector económico, no podríamos resaltar un patrón específico para las ellas que entran en una determinada cartera. Las empresas, que representan a sectores completamente diferentes, se incluyeron en ambas carteras.
Ahora vamos a mostrar las carteras “buenas” y “ malas” por separado. Utilizamos el método de cotización del portafolio (PQM), que se implementa en el comercio-analítico de terminales NetTradeX. Elegimos 10 activos de la cartera “buena” y expresamos su valor en dólares estadounidenses como estamos ahora interesados en el estudio de su valor absoluto. Para ello, se introduce un coeficiente de ponderación para cada activo en términos de dólares estadounidenses, al mismo tiempo que se respeta la proporción obtenida previamente en la solución de la cartera óptima. Por ejemplo, para las poblaciones de AXP estamos entrando en la cantidad de 897 dólares y para la población de VZ, el volumen de 8.177 dólares. A pesar de que el volumen se encuentra en dólares, y no en porcentajes, no afectará a la forma de la curva de la cartera, pero si sólo a las coordenadas. El gráfico es el siguiente:
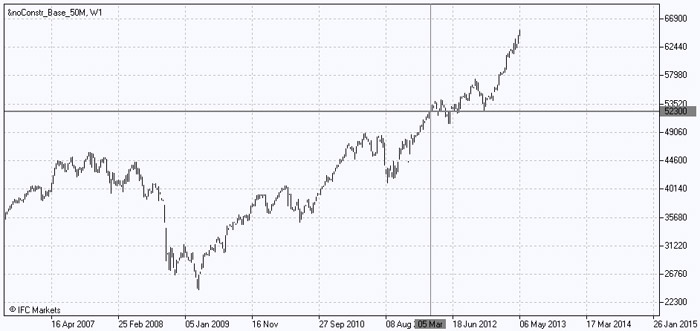
En general, tenemos una estructura de crecimiento retroespectivo. Desde principios de enero de 2009 el valor de la "buena" cartera aumentó en 2,5 veces, pero también debemos hablar de una caída significativa en el valor de la cartera en 2008. También debemos señalar que a principios de marzo 2012 el valor de la cartera fluctuó en torno a 52.300 dólares, hecho que nos ayudará en el futuro para el estudio de la dinámica de la cartera combinada.
Del mismo modo, vamos a construir “mala” cartera, que consta de 12 activos, y la introducción de los volúmenes correspondientes en dólares estadounidenses. Su dinámica retrospectiva, se presenta en el siguiente gráfico:
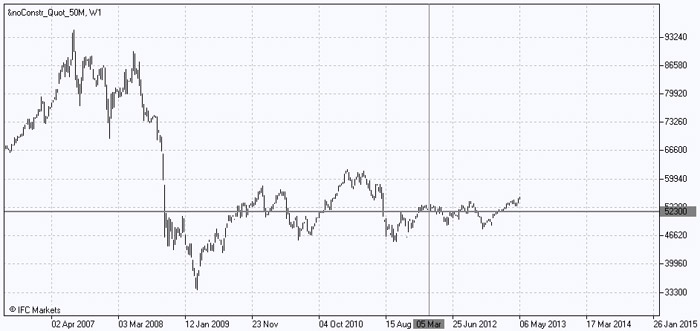
Obviamente, la cartera "mala" justifica su nombre, habiendo tenido un rendimiento significativamente inferior a la "buena" cartera, en términos de rentabilidad, lo cual es evidente a partir de la disminución de tres veces su valor en 2008 y el consiguiente leve crecimiento. Además, vamos a tener en cuenta que a principios de marzo de 2012, el valor de la cartera de "mala", también fluctuó en torno a 52.300 dólares.
Por último, vamos a construir una cartera combinada que incluirá tanto la "buenas" y la "malas" acciones, con los pesos obtenidos durante la optimización. Tenga en cuenta que los pesos negativos corresponden a las ventas en corto de las acciones. Cuando construimos una una cartera operando y analizando terminales NetTradeX, los activos con pesos positivos se incluirán en la parte baja de la cartera compuesta, mientras que los activos con pesas cortas - en la parte citada. En otras palabras, condicionalmente comprar activos "buenos" de la cartera y vender los activos de la "mala" - estas dos acciones reflejan la esencia del método PQM. El resultado es un coeficiente que refleja el valor de la primera (en nuestro caso - el "bueno") cartera en las unidades de la segunda ("mala"), y el gráfico nos permite hacer un seguimiento de sus cambios durante todo el período de tiempo:
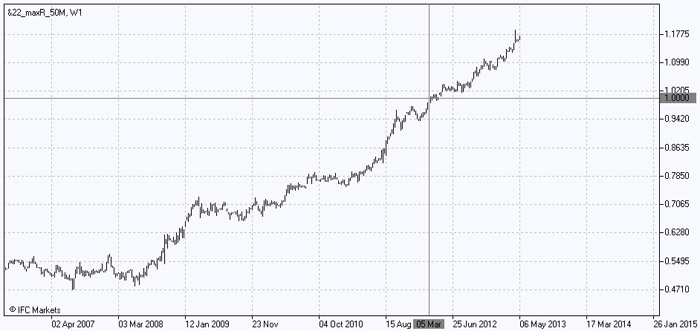
Milagrosamente, hemos recibido una estructura de crecimiento de la cartera combinada, que ha evitado cualquier caída significativa en 2008 y mostró un crecimiento continuo, leve y constante en el período post-crisis. Por otra parte, se puede observar que un importante crecimiento comenzó justo después de la crisis de 2008, lo que refleja diferentes grados en las respuestas de los activos, un factor global, y, de acuerdo con el gráfico, la importancia de este factor, así como las reacciones de las acciones son hasta ahora altas.
Los indicadores cuantitativos de desempeño de la cartera combinada se muestran en la siguiente tabla:
| Return | 7.52% |
| StDev | 6.40% |
| Sharpe | 1.18 |
Es fácil determinar el el retorno de la cartera, gracias a la posiciones cortas, mostrando que eran mucho más altos que los rendimientos individuales realizados de cualquiera de los demás activos (el rendimiento promedio máximo fue de 3.32%). La desviación estándar de la rentabilidad fue de 6,40%, que corresponde a los límites indicados. En su versión simplificada el coeficiente de Sharpe para la cartera es (1,18), lo que refleja su eficacia, es mucho más alto que los coeficientes de cualquiera de las 22 acciones (máximo coeficiente de Sharpe en su muestra sobre las poblaciones fue 0,39).
¿Cómo explicar el fuerte crecimiento de la cartera combinada así? Para responder a esta pregunta, tenemos que examinar el las carteras "malas" y "buenas" por separado. El procedimiento de optimización del peso ha permitido encontrar una combinación de posiciones largas y cortas en las acciones seleccionadas, lo que sería muy coherente con nuestra tal estrategia de inversión. Utilizando el método PQM y su módulo en la terminal NetTradeX, hemos sido capaces de seguir la dinámica de ambas carteras individualmente y su versión combinada.
El análisis del comportamiento de la cartera muestra que durante la crisis más grave en 2008, las "buenas" carteras perdieron menos valor que el de las "malas". En el período posterior a la crisis, el crecimiento de la primera cartera también demostró ser más prominente que el crecimiento de la segunda. Mediante la combinación de estos dos factores, se obtuvo una estructura de crecimiento continuo. Puesto que el crecimiento de la cartera combinada se inició en 2008 (antes de que el portafolio combinado haya seguido una tendencia neutral), podemos suponer que este año se ha convertido en el punto de inversión, cuando las acciones han comenzado a mostrar diferentes grados de reacciones a algunos factores sistemáticos. Tenga en cuenta que antes de principios de marzo de 2012, el valor de la cartera “mala" ha sido superior al valor de la "buena" cartera - el coeficiente de las versiones combinadas fue inferior a 1. Sin embargo, en Marzo de 2012, su valor absoluto se igualo, y el coeficiente de dilatación fue igual a 1. Posteriormente más y más unidades de la cartera “mala" estaban obligadas a comprar una unidad de la "buena” cartera.
Artículos previos
- El cuarto postulado de la Teoría de Dow: sirviendo al inversor
- Spread de portafolio a base de futuros continuos
- Portfolio de Sharpe – "Tres Líderes"
- Optimización del Portfolio a través del Método PQM (Parte 2)
- Optimización del Portafolio a través del Método PQM (Parte 1)
- Construcción y Análisis de Portafolios de Acciones con el Método de Cotización del Portafolio PQM
